flowchart TB Boost(Boost) --> math(math) Eigen(Eigen) --> math(math) OpenCL(OpenCL) --> math(math) SUNDIALS(SUNDIALS) --> math(math) oneTBB(oneTBB) --> math(math) math(math) --> Stan(Stan) Stan(Stan) --> CmdStan(CmdStan) Stan(Stan) --> RStan(RStan) RStan --> rstanarm(rstanarm) RStan --> brms(brms) RStan --> prophet(prophet) CmdStan --> CmdStanR(CmdStanR) CmdStan --> CmdStanPy(CmdStanPy) CmdStan --> MathematicaStan(MathematicaStan)
31 概率推理框架
\[ \def\bm#1{{\boldsymbol #1}} \]
Stan 是一个贝叶斯统计建模和计算的概率推理框架,也是一门用于贝叶斯推断和优化的概率编程语言 (Gelman, Lee, 和 Guo 2015; Carpenter 等 2017)。它使用汉密尔顿蒙特卡罗算法(Hamiltonian Monte Carlo algorithm ,简称 HMC 算法)抽样,内置一种可以自适应调整采样步长的 No-U-Turn sampler (简称 NUTS 采样器) 。Stan 还提供自动微分变分推断(Automatic Differentiation Variational Inference algorithm 简称 ADVI 算法)算法做近似贝叶斯推断获取参数的后验分布,以及拟牛顿法(the limited memory Broyden-Fletcher-Goldfarb-Shanno algorithm 简称 L-BFGS 算法)优化算法获取参数的惩罚极大似然估计。
经过 10 多年的发展,Stan 已经形成一个相对成熟的生态,它提供统计建模、数据分析和预测能力,广泛应用于社会、生物、物理、工程、商业等领域,在学术界和工业界的影响力也不小。下 图 31.1 是 Stan 生态中各组件依赖架构图,math 库是 Stan 框架最核心的组件,它基于 Boost 、Eigen 、OpenCL 、SUNDIALS 和 oneTBB 等诸多 C++ 库,提供概率推理、自动微分、矩阵计算、并行计算、GPU 计算和求解代数微分方程等功能。
CmdStan 是 Stan 的命令行接口,可在 MacOS / Linux 的终端软件,Windows 的命令行窗口或 PowerShell 软件中使用。CmdStanR、CmdStanPy 和 MathematicaStan 分别是 CmdStan 的 R 语言、Python 语言和 Mathematica 语言接口。每次当 Stan 发布新版本时,CmdStan 也会随之发布新版,只需指定新的 CmdStan 安装路径,CmdStanR 就可以使用上,CmdStanR 包与 Stan 是相互独立的更新机制。 CmdStanR 负责处理 CmdStan 运行的结果,而编译代码,生成模型和模拟采样等都是由 CmdStan 完成。入门 CmdStanR 后,可以快速转入对 Stan 底层原理的学习,有利于编码符合实际需要的复杂模型,有利于掌握常用的炼丹技巧,提高科研和工作的效率。
rstan 是 Stan 的 R 语言接口,该接口依赖 Rcpp、RcppEigen、BH、RcppParallel 和 StanHeaders 等 R 包,由于存在众多上游 R 包依赖,RStan 的更新通常滞后于 Stan 的更新,而且滞后很多,不利于及时地使用最新的学术研究成果。 因此,相比于 rstan 包,CmdStanR 更加轻量,可以更快地将 CmdStan 的新功能融入进来,cmdstanr 和 CmdStan 是分离的,方便用户升级和维护。
rstanarm 和 brms 是 RStan 的扩展包,各自提供了一套用于表示统计模型的公式语法。它们都支持丰富的统计模型,比如线性模型、广义线性模型、线性混合效应模型、广义线性混合效应模型等。相比于 rstan, 它们使用起来更加方便,因为它内置了大量统计模型的 Stan 实现,即将公式语法翻译成 Stan 编码的模型,然后调用 rstan 或 cmdstanr 翻译成 C++,最后编译成动态链接库。除了依赖 rstan 包,rstanarm 和 brms 还依赖大量其它 R 包,因此,安装、更新都比较麻烦。
顺便一提,类似的用于概率推理和统计分析的框架,还有 Python 社区的 PyMC3 和 TensorFlow Probability。
31.1 Stan 入门
31.1.1 Stan 的基础语法
下面以一个简单示例介绍 Stan 的用法,包括 Stan 的基本用法、变量类型、代码结构等,
考虑一个已知方差的正态分布,设 \(-3, -2, -1, 0, 1, 2, 3\) 是取自正态分布 \(\mathcal{N}(\mu,1)\) 的一个样本,也是取自该正态分布的一组随机数。现在的问题是估计该正态分布的均值参数 \(\mu\) 。Stan 编码的正态分布模型如下:
transformed data代码块是一组已知的数据,这部分数据是不需要从外部传递进来的。这个样本是以向量存储的,需要声明向量的长度和类型(默认类型是实数),每一行以分号结尾,这与 C++ 的语法一样。parameters代码块是未知的参数,需要声明各个参数的类型。这里只有一个参数,且只是一个未知的实数,声明类型即可。model代码块是抽样语句表示的模型结构,符号~表示服从的意思,函数y ~ normal(mu, 1)是正态分布的抽样语句。
接下来,编译 Stan 代码,准备参数初值,配置采样的参数。首先加载 cmdstanr 包,设置 2 条迭代链,给每条链设置相同的参数初始值。代码编译后,生成一个模型对象 mod_gaussian,接着,调用方法 sample() ,传递迭代初值 init,初始化阶段的迭代次数 iter_warmup ,采样阶段的迭代次数 iter_sampling,采样的链条数 chains 及并行时 分配的 CPU 核心数 parallel_chains ,随机数种子 seed 。
library(cmdstanr)
nchains <- 2 # 2 条迭代链
# 给每条链设置相同的参数初始值
inits_data_gaussian <- lapply(1:nchains, function(i) {
list(
mu = 1
)
})
fit_gaussian <- mod_gaussian$sample(
init = inits_data_gaussian, # 迭代初值
iter_warmup = 200, # 每条链初始化迭代次数
iter_sampling = 200, # 每条链采样迭代次数
chains = nchains, # 马尔科夫链的数目
parallel_chains = nchains,# 指定 CPU 核心数,可以给每条链分配一个
seed = 20232023 # 设置随机数种子,不要使用 set.seed() 函数
)#> Running MCMC with 2 parallel chains...
#>
#> Chain 1 Iteration: 1 / 400 [ 0%] (Warmup)
#> Chain 1 Iteration: 100 / 400 [ 25%] (Warmup)
#> Chain 1 Iteration: 200 / 400 [ 50%] (Warmup)
#> Chain 1 Iteration: 201 / 400 [ 50%] (Sampling)
#> Chain 1 Iteration: 300 / 400 [ 75%] (Sampling)
#> Chain 1 Iteration: 400 / 400 [100%] (Sampling)
#> Chain 2 Iteration: 1 / 400 [ 0%] (Warmup)
#> Chain 2 Iteration: 100 / 400 [ 25%] (Warmup)
#> Chain 2 Iteration: 200 / 400 [ 50%] (Warmup)
#> Chain 2 Iteration: 201 / 400 [ 50%] (Sampling)
#> Chain 2 Iteration: 300 / 400 [ 75%] (Sampling)
#> Chain 2 Iteration: 400 / 400 [100%] (Sampling)
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#>
#> Both chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.3 seconds.默认情况下,采样过程中会输出一些信息,以上是 2 条链并行采样的过程,给出百分比进度及时间消耗。采样完成后,调用方法 summary() 汇总和展示采样结果。
#> # A tibble: 2 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <num> <num> <num> <num> <num> <num> <num> <num> <num>
#> 1 lp__ -14.4 -14.2 0.708 0.212 -15.6 -14.0 1.01 177. 220.
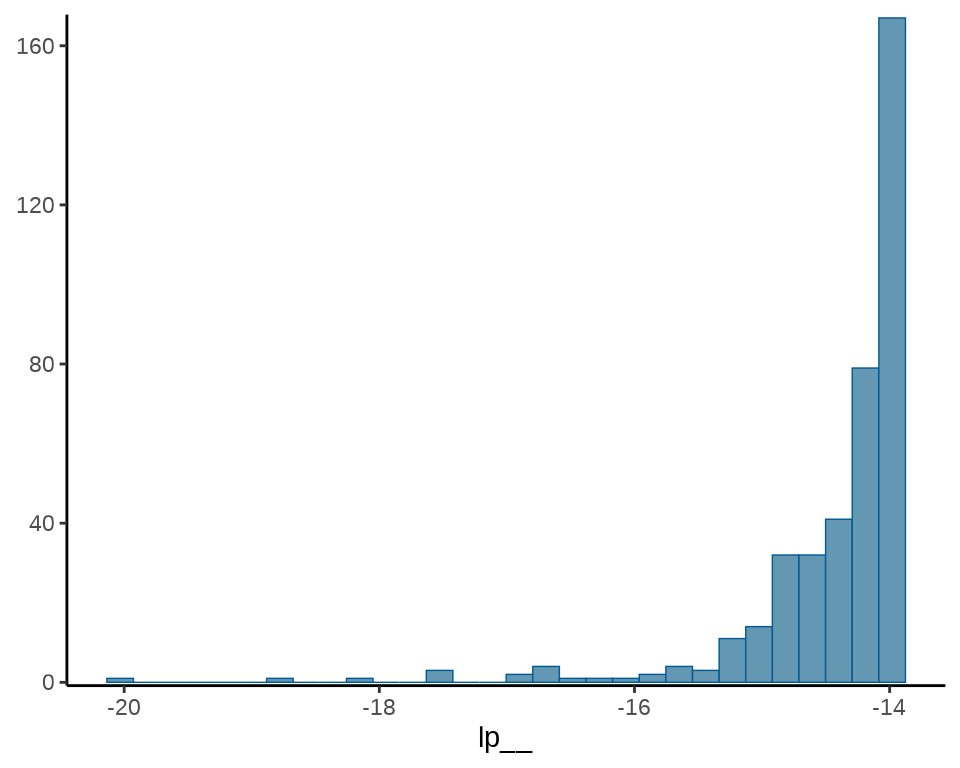
#> 2 mu 0.0365 0.0307 0.348 0.298 -0.511 0.572 1.01 229. 173.输出模型中各个参数的后验分布的一些统计量,如均值(mean)、中位数(median)、标准差(sd),0.05 分位点(q5),0.95 分位点(q95)等。此外,还有 lp__ 后验对数概率密度值,每个模型都会有该值。summary() 方法有一些参数可以控制数字的显示方式和精度。下面展示的是保留 4 位有效数字的结果。
#> # A tibble: 2 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk
#> <chr> <dec:4> <dec:4> <dec:4> <dec:4> <dec:4> <dec:4> <dec:> <dec:4>
#> 1 lp__ -14.43 -14.15 0.7083 0.2118 -15.60 -14.00 1.007 177.2
#> 2 mu 0.03647 0.03073 0.3476 0.2978 -0.5115 0.5722 1.007 229.0
#> # ℹ 1 more variable: ess_tail <dec:4>接下来,要介绍 Stan 代码中的保留字 target 的含义,因为它在 Stan 代码中很常见,与输出结果中的 lp__ 一行紧密相关。
-
lp__表示后验概率密度函数的对数。 - target 累加一些和参数无关的数不影响参数的估计,但影响
lp__的值。 - 抽样语句表示模型会扔掉后验概率密度函数的对数的常数项。
为此,不妨在之前的 Stan 代码的基础上添加两行,新的 Stan 代码如下:
接着,再次编译代码、采样,为了节约篇幅,设置两个参数 show_messages 和 refresh ,不显示中间过程和采样进度。其它参数设置不变,代码如下:
fit_gaussian <- mod_gaussian_target$sample(
init = inits_data_gaussian,
iter_warmup = 200,
iter_sampling = 200,
chains = nchains,
parallel_chains = nchains,
show_messages = FALSE, # 不显示中间过程
refresh = 0, # 不显示采样进度
seed = 20232023
)
fit_gaussian$summary(.num_args = list(sigfig = 4, notation = "dec"))#> # A tibble: 2 × 10
#> variable mean median sd mad q5 q95 rhat
#> <chr> <dec:4> <dec:4> <dec:4> <dec:4> <dec:4> <dec:4> <dec:4>
#> 1 lp__ 12335. 12335. 0.7074 0.1483 12334. 12336. 1.008
#> 2 mu 0.03647 0.03073 0.3476 0.2978 -0.5115 0.5722 1.007
#> # ℹ 2 more variables: ess_bulk <dec:4>, ess_tail <dec:4>可以清楚地看到 lp__ 的值发生了变化,而参数 mu 的值没有变化。这是因为抽样语句 y ~ normal(mu, 1); 隐含一个 lp__ ,target 指代 lp__ 的值,符号 += 表示累加。两次累加后得到 12335.09。
下面从概率密度函数出发,用 R 语言来计算逐点对数似然函数值。一般地,不妨设 \(x_1,x_2,\cdots,x_n\) 是来自正态总体 \(\mathcal{N}(\mu,1)\) 的一个样本。则正态分布的概率密度函数 \(f(x)\) 的对数如下:
\[ \log f(x) = \log \frac{1}{\sqrt{2\pi}} - \frac{(x - \mu)^2}{2} \]
已知参数 \(\mu\) 是一个非常接近 0 的数,不妨将 \(\mu = 0\) 代入计算。
去掉常数项后,计算概率密度函数值的对数和。
这就比较接近原 lp__ 的值了,所以,lp__ 表示后验概率密度函数的对数,扔掉了与参数无关的常数项。若以概率密度函数的对数 normal_lpdf 替代抽样语句,则常数项是保留的。normal_lpdf 是 Stan 内置的函数,输入值为随机变量的取值 y 、位置参数 mu 和尺度参数 sigma,返回值为 real 实数。
real normal_lpdf(reals y | reals mu, reals sigma)
接着,编译上述代码以及重复采样的步骤,参数设置也一样。
fit_gaussian <- mod_gaussian_lpdf$sample(
init = inits_data_gaussian,
iter_warmup = 200,
iter_sampling = 200,
chains = nchains,
parallel_chains = nchains,
show_messages = FALSE,
refresh = 0,
seed = 20232023
)
fit_gaussian$summary(.num_args = list(sigfig = 4, notation = "dec"))#> # A tibble: 2 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk
#> <chr> <dec:4> <dec:4> <dec:4> <dec:4> <dec:4> <dec:4> <dec:> <dec:4>
#> 1 lp__ -20.86 -20.58 0.7083 0.2119 -22.03 -20.43 1.007 176.7
#> 2 mu 0.03647 0.03073 0.3476 0.2978 -0.5115 0.5722 1.007 229.0
#> # ℹ 1 more variable: ess_tail <dec:4>可以看到,此时 lp__ 的值包含常数项,两种表示方式对参数的计算结果没有影响。
31.1.2 Stan 的变量类型
变量的声明没有太多的内涵,就是 C++ 和 Stan 定义的语法,比如整型用 int 声明。建模过程中,时常需要将 R 语言环境中的数据传递给 Stan 代码编译出来的模型,而 Stan 是基于 C++ 语言,在变量类型方面有继承有发展。下表给出 Stan 与 R 语言中的变量类型对应关系。值得注意, R 语言的类型检查是不严格的,使用变量也不需要提前声明和初始化。Stan 语言中向量、矩阵的类型都是实数,下标也从 1 开始,元组类型和 R 语言中的列表类似,所有向量默认都是列向量。
| 变量类型 | Stan 语言 | R 语言 |
|---|---|---|
| 整型 | int x = 1; |
x = 1L |
| 实数 | real x = 3.14; |
x = 3.14 |
| 向量 | vector[3] x = [1, 2, 3]'; |
x = c(1L, 2L, 3L) |
| 矩阵 | matrix[3,1] x; |
matrix(data = c(1L, 2L, 3L)) |
| 数组 | array[3] int x; |
array(data = c(1L, 2L, 3L), dim = c(3, 1, 1)) |
| 元组 | tuple(vector[3]) x; |
list(x = c(1L, 2L, 3L)) |
31.1.3 Stan 的代码结构
functions {
// ... function declarations and definitions ...
}
data {
// ... declarations ...
}
transformed data {
// ... declarations ... statements ...
}
parameters {
// ... declarations ...
}
transformed parameters {
// ... declarations ... statements ...
}
model {
// ... declarations ... statements ...
}
generated quantities {
// ... declarations ... statements ...
}31.2 选择先验分布
考虑一个响应变量服从伯努利分布的广义线性模型。
\[ \begin{aligned} &\boldsymbol{y} \sim \mathrm{Bernoulli}(\boldsymbol{p}) \\ &\mathrm{logit}(\boldsymbol{p}) = \log (\frac{\boldsymbol{p}}{1-\boldsymbol{p}})= \alpha + X \boldsymbol{\beta} \end{aligned} \]
下面模拟生成 2500 个样本,其中 10 个正态协变量,非 0 的回归系数是截距 \(\alpha = 1\) 和向量 \(\boldsymbol{\beta}\) 中的 \(\beta_1 = 3,\beta_2 = -2\) 。对模型实际有用的是 3 个变量,采用贝叶斯建模,其它变量应该被收缩掉。贝叶斯收缩 (Bayesian shrinkage)与变量选择 (Variable selection) 是有关系的,先验分布影响收缩的力度。
在贝叶斯先验分布中,有几个常用的概率分布,分别是正态分布、拉普拉斯分布(双指数分布)、柯西分布,下图集中展示了这几个的标准分布。
代码
dlaplace <- function(x, mu = 0, sigma = 1) {
1 / (2*sigma) * exp(- abs(x - mu) / sigma)
}
ggplot() +
geom_function(
fun = dnorm, args = list(mean = 0, sd = 1),
aes(colour = "正态分布"), linewidth = 1.2, xlim = c(-6, 6)
) +
geom_function(
fun = dlaplace, args = list(mu = 0, sigma = 1),
aes(colour = "拉普拉斯分布"), linewidth = 1.2, xlim = c(-6, 6)
) +
geom_function(
fun = dcauchy, args = list(location = 0, scale = 0.5),
aes(colour = "柯西分布"), linewidth = 1.2, xlim = c(-6, 6)
) +
theme_classic() +
theme(legend.position = c(0.9, 0.9)) +
labs(x = "$x$", y = "$f(x)$", colour = NULL)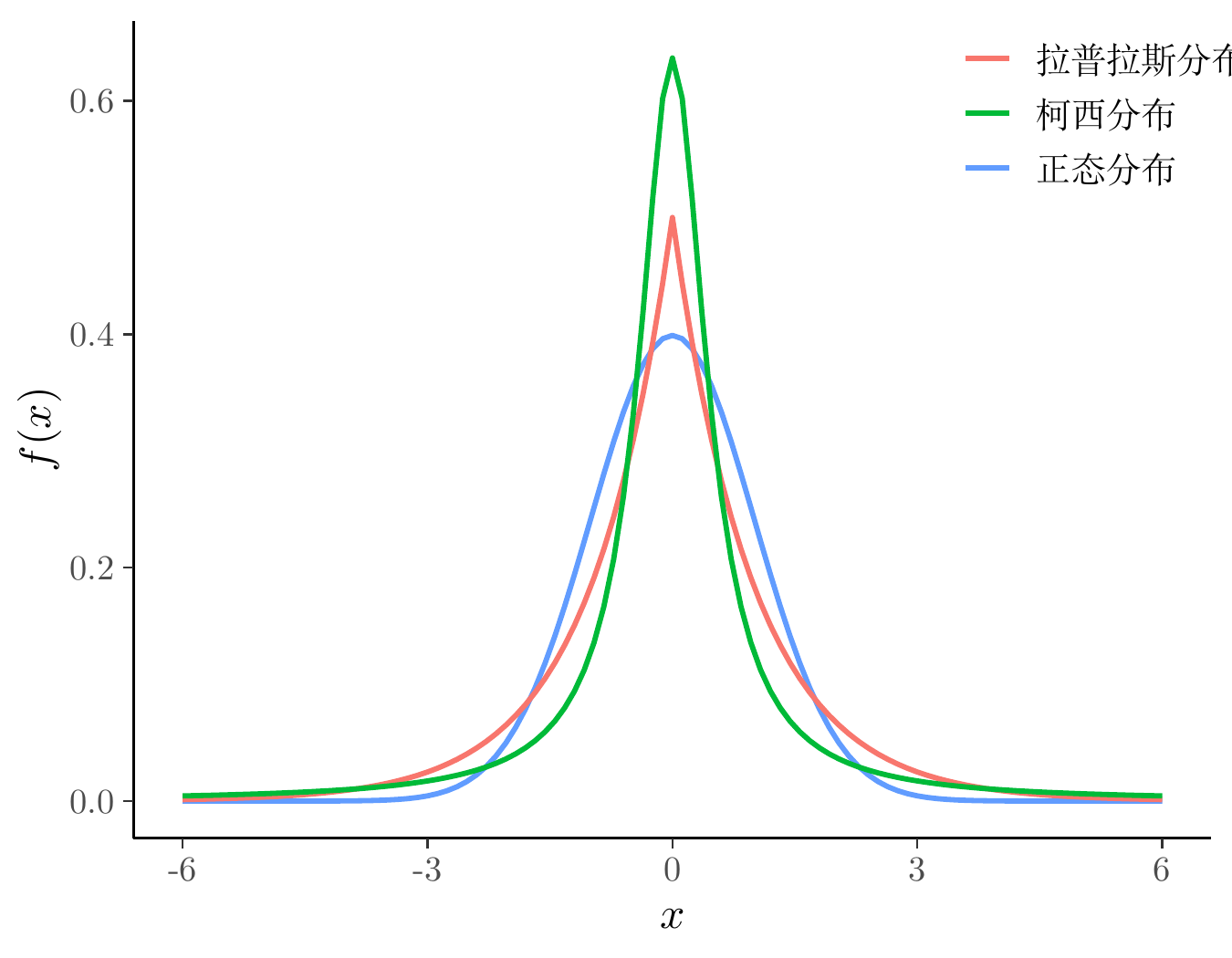
接下来,考虑几种常见的先验设置。
31.2.1 正态先验
指定回归系数 \(\alpha,\beta\) 的先验分布如下
\[ \begin{aligned} \alpha &\sim \mathcal{N}(0, 1000) \\ \beta &\sim \mathcal{N}(0, 1000) \end{aligned} \]
正态分布中设置相当大的方差意味着分布相当扁平, \(\alpha,\beta\) 的取值在区间 \((-\infty,+\infty)\) 上比较均匀。
data {
int<lower=1> k;
int<lower=0> n;
matrix[n, k] X;
array[n] int<lower=0, upper=1> y;
}
parameters {
vector[k] beta;
real alpha;
}
model {
target += normal_lpdf(beta | 0, 1000);
target += normal_lpdf(alpha | 0, 1000);
target += bernoulli_logit_glm_lpmf(y | X, alpha, beta);
}
generated quantities {
vector[n] log_lik;
for (i in 1 : n) {
log_lik[i] = bernoulli_logit_lpmf(y[i] | alpha + X[i] * beta);
}
}mod_logit_normal <- cmdstan_model(
stan_file = "code/bernoulli_logit_glm_normal.stan",
compile = TRUE, cpp_options = list(stan_threads = TRUE)
)
fit_logit_normal <- mod_logit_normal$sample(
data = mdata,
chains = 2,
parallel_chains = 2,
iter_warmup = 1000,
iter_sampling = 1000,
threads_per_chain = 2,
seed = 20232023,
show_messages = FALSE,
refresh = 0
)
# 输出结果
fit_logit_normal$summary(c("alpha", "beta", "lp__"))#> # A tibble: 12 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk
#> <chr> <num> <num> <num> <num> <num> <num> <num> <num>
#> 1 alpha 1.02 1.02 0.0710 0.0699 0.902 1.13e+0 1.00 2648.
#> 2 beta[1] 3.14 3.13 0.136 0.139 2.92 3.37e+0 1.00 2054.
#> 3 beta[2] -2.03 -2.03 0.0994 0.0992 -2.19 -1.87e+0 1.00 2041.
#> 4 beta[3] 0.0604 0.0609 0.0663 0.0667 -0.0455 1.70e-1 1.00 3339.
#> 5 beta[4] -0.0266 -0.0244 0.0665 0.0655 -0.140 8.30e-2 0.999 3548.
#> 6 beta[5] 0.0146 0.0174 0.0674 0.0689 -0.0969 1.24e-1 1.00 4352.
#> 7 beta[6] 0.0215 0.0231 0.0655 0.0652 -0.0862 1.26e-1 1.00 3111.
#> 8 beta[7] 0.103 0.105 0.0611 0.0600 0.00131 2.02e-1 1.00 3377.
#> 9 beta[8] -0.0303 -0.0312 0.0649 0.0600 -0.138 7.59e-2 1.00 3577.
#> 10 beta[9] -0.0882 -0.0873 0.0660 0.0666 -0.194 2.09e-2 1.00 3487.
#> 11 beta[10] 0.0814 0.0803 0.0647 0.0653 -0.0237 1.86e-1 1.00 4377.
#> 12 lp__ -843. -842. 2.38 2.25 -847. -8.39e+2 1.00 800.
#> # ℹ 1 more variable: ess_tail <num>31.2.2 Lasso 先验
指定回归系数 \(\alpha,\beta\) 的先验分布如下
\[ \begin{aligned} \lambda &\sim \mathrm{Half\_Cauchy}(0,0.01) \\ \alpha &\sim \mathrm{Double\_exponential}(0, \lambda) \\ \beta &\sim \mathrm{Double\_exponential}(0, \lambda) \end{aligned} \]
其中, \(\alpha,\beta\) 服从双指数分布,惩罚因子 \(\lambda\) 服从柯西分布。顺便一提,若把双指数分布改为正态分布,则 Lasso 先验变为岭先验。相比于岭先验,Lasso 先验有意将回归系数往 0 上收缩,这非常类似于频率派中的岭回归与 Lasso 回归的关系。
data {
int<lower=1> k;
int<lower=0> n;
matrix[n, k] X;
array[n] int<lower=0, upper=1> y;
}
parameters {
vector[k] beta;
real alpha;
real<lower=0> lambda;
}
model {
target += double_exponential_lpdf(beta | 0, lambda);
target += double_exponential_lpdf(alpha | 0, lambda);
target += cauchy_lpdf(lambda | 0, 0.01);
target += bernoulli_logit_glm_lpmf(y | X, alpha, beta);
}
generated quantities {
vector[n] log_lik;
for (i in 1 : n) {
log_lik[i] = bernoulli_logit_lpmf(y[i] | alpha + X[i] * beta);
}
}mod_logit_lasso <- cmdstan_model(
stan_file = "code/bernoulli_logit_glm_lasso.stan",
compile = TRUE, cpp_options = list(stan_threads = TRUE)
)
fit_logit_lasso <- mod_logit_lasso$sample(
data = mdata,
chains = 2,
parallel_chains = 2,
iter_warmup = 1000,
iter_sampling = 1000,
threads_per_chain = 2,
seed = 20232023,
show_messages = FALSE,
refresh = 0
)
# 输出结果
fit_logit_lasso$summary(c("alpha", "beta", "lambda", "lp__"))#> # A tibble: 13 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk
#> <chr> <num> <num> <num> <num> <num> <num> <num> <num>
#> 1 alpha 0.993 0.994 0.0756 0.0782 0.871 1.12e+0 1.00 2117.
#> 2 beta[1] 3.08 3.08 0.135 0.137 2.87 3.31e+0 1.00 1910.
#> 3 beta[2] -1.99 -1.99 0.0975 0.0949 -2.15 -1.82e+0 1.00 1926.
#> 4 beta[3] 0.0539 0.0508 0.0623 0.0645 -0.0430 1.59e-1 1.00 3336.
#> 5 beta[4] -0.0223 -0.0212 0.0615 0.0638 -0.122 7.95e-2 1.00 3525.
#> 6 beta[5] 0.0108 0.0105 0.0651 0.0647 -0.0977 1.20e-1 1.00 4587.
#> 7 beta[6] 0.0191 0.0183 0.0592 0.0623 -0.0767 1.20e-1 1.00 3167.
#> 8 beta[7] 0.0940 0.0937 0.0629 0.0621 -0.00795 1.95e-1 1.00 2785.
#> 9 beta[8] -0.0256 -0.0251 0.0612 0.0629 -0.129 7.35e-2 1.00 3390.
#> 10 beta[9] -0.0801 -0.0793 0.0621 0.0635 -0.182 2.06e-2 1.00 2988.
#> 11 beta[10] 0.0743 0.0734 0.0622 0.0632 -0.0241 1.78e-1 1.00 3208.
#> 12 lambda 0.599 0.564 0.201 0.162 0.355 9.73e-1 1.00 2921.
#> 13 lp__ -775. -775. 2.44 2.42 -779. -7.72e+2 1.00 795.
#> # ℹ 1 more variable: ess_tail <num>计算 LOO-CV 比较正态先验和 Lasso 先验
fit_logit_normal_loo <- fit_logit_normal$loo(variables = "log_lik", cores = 2)
print(fit_logit_normal_loo)#>
#> Computed from 2000 by 2500 log-likelihood matrix
#>
#> Estimate SE
#> elpd_loo -762.2 27.3
#> p_loo 11.2 0.5
#> looic 1524.4 54.5
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#>
#> All Pareto k estimates are good (k < 0.5).
#> See help('pareto-k-diagnostic') for details.fit_logit_lasso_loo <- fit_logit_lasso$loo(variables = "log_lik", cores = 2)
print(fit_logit_lasso_loo)#>
#> Computed from 2000 by 2500 log-likelihood matrix
#>
#> Estimate SE
#> elpd_loo -761.6 26.8
#> p_loo 10.5 0.5
#> looic 1523.3 53.7
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#>
#> All Pareto k estimates are good (k < 0.5).
#> See help('pareto-k-diagnostic') for details.loo 包的函数 loo_compare() 比较两个模型
#> elpd_diff se_diff
#> model1 0.0 0.0
#> model0 -0.6 0.5输出结果中最好的模型放在第一行。LOOIC 越小越好,所以,Lasso 先验更好。
31.2.3 Horseshoe 先验
Horseshoe 先验(Horse shoe)指定回归系数 \(\alpha,\bm{\beta}\) 的先验分布如下
\[ \begin{aligned} \lambda_i &\sim \mathrm{Half\_Cauchy}(0,1) \\ \alpha | \lambda_0,\tau &\sim \mathcal{N}(0, \tau^2\lambda_0^2) \\ \beta_i | \lambda_i,\tau &\sim \mathcal{N}(0, \tau^2\lambda_i^2),\quad i = 1,2,\cdots,10 \end{aligned} \]
其中,\(\tau\) 称之为全局超参数,它将所有的回归系数朝着 0 收缩。而作用在局部超参数 \(\lambda_i\) 上的重尾柯西先验允许某些回归系数逃脱收缩。
data {
int<lower=1> k;
int<lower=0> n;
matrix[n, k] X;
array[n] int<lower=0, upper=1> y;
}
parameters {
vector[k] beta_tilde;
real alpha;
real<lower=0> tau;
vector<lower=0>[k] lambda;
}
transformed parameters {
vector[k] beta = beta_tilde .* lambda * tau;
}
model {
target += normal_lpdf(beta_tilde | 0, lambda);
target += normal_lpdf(alpha | 0, lambda);
target += cauchy_lpdf(tau | 0, 1);
target += cauchy_lpdf(lambda | 0, 1);
target += bernoulli_logit_glm_lpmf(y | X, alpha, beta);
}
generated quantities {
vector[n] log_lik;
for (i in 1 : n) {
log_lik[i] = bernoulli_logit_lpmf(y[i] | alpha + X[i] * beta);
}
}# horseshoe 先验
mod_logit_horseshoe <- cmdstan_model(
stan_file = "code/bernoulli_logit_glm_horseshoe.stan",
compile = TRUE, cpp_options = list(stan_threads = TRUE)
)
fit_logit_horseshoe <- mod_logit_horseshoe$sample(
data = mdata,
chains = 2,
parallel_chains = 2,
iter_warmup = 1000,
iter_sampling = 1000,
threads_per_chain = 2,
seed = 20232023,
show_messages = FALSE,
refresh = 0
)
fit_logit_horseshoe$summary(c("alpha", "beta", "tau", "lambda", "lp__")) #> # A tibble: 23 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk
#> <chr> <num> <num> <num> <num> <num> <num> <num> <num>
#> 1 alpha 0.933 0.930 0.0759 0.0748 0.810 1.07 1.00 1303.
#> 2 beta[1] 3.04 3.04 0.138 0.139 2.82 3.27 1.00 1613.
#> 3 beta[2] -1.97 -1.96 0.102 0.102 -2.14 -1.81 1.01 1756.
#> 4 beta[3] 0.0285 0.0225 0.0468 0.0399 -0.0391 0.118 1.00 1655.
#> 5 beta[4] -0.0125 -0.00787 0.0440 0.0352 -0.0898 0.0534 1.00 1814.
#> 6 beta[5] 0.00722 0.00434 0.0438 0.0357 -0.0630 0.0871 1.00 1703.
#> 7 beta[6] 0.00901 0.00619 0.0441 0.0347 -0.0595 0.0852 1.00 2334.
#> 8 beta[7] 0.0590 0.0516 0.0567 0.0576 -0.0186 0.161 1.00 1052.
#> 9 beta[8] -0.0134 -0.00789 0.0446 0.0354 -0.0910 0.0537 1.00 1509.
#> 10 beta[9] -0.0478 -0.0383 0.0555 0.0518 -0.151 0.0251 1.00 1694.
#> # ℹ 13 more rows
#> # ℹ 1 more variable: ess_tail <num>可以看到回归系数小的压缩效果很明显,而回归系数大的几乎没有压缩。
fit_logit_horseshoe_loo <- fit_logit_horseshoe$loo(variables = "log_lik", cores = 2)
print(fit_logit_horseshoe_loo)#>
#> Computed from 2000 by 2500 log-likelihood matrix
#>
#> Estimate SE
#> elpd_loo -760.1 26.5
#> p_loo 7.7 0.4
#> looic 1520.2 53.0
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#>
#> All Pareto k estimates are good (k < 0.5).
#> See help('pareto-k-diagnostic') for details.LOOIC 比之 Lasso 先验的情况更小了。
brms 包(版本 2.20.1)在模型中全局性地使用 horseshoe 先验信息。
31.2.4 SpikeSlab 先验
SpikeSlab 先验(Spike Slab)放在非 0 协变量的个数上,是离散的先验。
31.3 选择推理算法
开篇提及 Stan 内置了多种推理算法,不同的算法获得的结果是存在差异的。
- full Bayesian statistical inference with MCMC sampling (NUTS, HMC)
- approximate Bayesian inference with variational inference (ADVI)
- penalized maximum likelihood estimation with optimization (L-BFGS)
31.3.1 惩罚极大似然算法
L-BFGS 算法拟合模型,速度非常快。
# L-BFGS 算法拟合模型
fit_optim_logit <- mod_logit_lasso$optimize(
data = mdata, # 观测数据
init = 0, # 所有参数初值设为 0
refresh = 0, # 不显示迭代进程
algorithm = "lbfgs", # 优化器
threads = 1, # 单线程
seed = 20232023 # 随机数种子
)#> Finished in 0.2 seconds.#> # A tibble: 13 × 2
#> variable estimate
#> <chr> <num>
#> 1 alpha 0.981
#> 2 beta[1] 3.05
#> 3 beta[2] -1.96
#> 4 beta[3] 0.0488
#> 5 beta[4] -0.0166
#> 6 beta[5] 0.00528
#> 7 beta[6] 0.0126
#> 8 beta[7] 0.0923
#> 9 beta[8] -0.0204
#> 10 beta[9] -0.0777
#> 11 beta[10] 0.0721
#> 12 lambda 0.488
#> 13 lp__ -768.31.3.2 变分近似推断算法
ADVI 算法拟合模型,可选的优化器有 meanfield 和 fullrank ,相比于 L-BFGS 稍慢
# ADVI 算法拟合模型
fit_advi_logit <- mod_logit_lasso$variational(
data = mdata, # 观测数据
init = 0, # 所有参数初值设为 0
refresh = 0, # 不显示迭代进程
algorithm = "meanfield", # 优化器
threads = 1, # 单线程
seed = 20232023 # 随机数种子
)#> Finished in 1.5 seconds.#> # A tibble: 13 × 7
#> variable mean median sd mad q5 q95
#> <chr> <num> <num> <num> <num> <num> <num>
#> 1 alpha 1.02 1.02 0.0615 0.0630 0.914 1.11
#> 2 beta[1] 3.07 3.07 0.0899 0.0870 2.93 3.22
#> 3 beta[2] -1.98 -1.98 0.0675 0.0666 -2.08 -1.86
#> 4 beta[3] 0.0161 0.0159 0.0678 0.0670 -0.0945 0.129
#> 5 beta[4] -0.0199 -0.0221 0.0639 0.0621 -0.121 0.0857
#> 6 beta[5] -0.00128 -0.00202 0.0722 0.0713 -0.116 0.121
#> 7 beta[6] -0.0423 -0.0446 0.0705 0.0689 -0.156 0.0754
#> 8 beta[7] 0.0760 0.0750 0.0490 0.0489 -0.00517 0.152
#> 9 beta[8] -0.0742 -0.0752 0.0659 0.0637 -0.181 0.0347
#> 10 beta[9] -0.0495 -0.0501 0.0802 0.0818 -0.185 0.0805
#> 11 beta[10] 0.0444 0.0440 0.0520 0.0522 -0.0444 0.128
#> 12 lambda 0.698 0.662 0.243 0.228 0.379 1.13
#> 13 lp__ -777. -777. 3.39 3.22 -783. -773.31.3.3 拉普拉斯近似算法
CmdStan 已经集成,但 cmdstanr 包对该算法的支持还在开发中。